The relationship of music and mathematics are well documented since the time of ancient Greece, and this relationship is evidenced in the mathematical or quasi-mathematical nature of compositional approaches by composers such as Xenakis, Schoenberg, Charles Dodge, and composers who employ computer-assisted-composition techniques in their work. This study is an attempt to create a composition with data collected over the course 32 years from melting glaciers in seven areas in Greenland, and at the same time produce a work that is expressive and expands my compositional palette. To begin with, numeric values from data were rounded to four-digits and converted into frequencies in Hz. Moreover, the other data are rounded to two-digit values that determine note durations. Using these transformations, a prototype composition was developed, with data from each of the seven Greenland-glacier areas used to compose individual instrument parts in a septet. The composition Contrast and Conflict is a pilot study based on 20 data sets. Serves as a practical example of the methods the author used to develop and transform data. One of the author’s significant findings is that data analysis, albeit sometimes painful and time-consuming, reduced his overall composing time. The variety and richness of data that exists from all academic areas and disciplines conceivably provide a rich reservoir of material from which to fashion compositions. As more composers explore this avenue of work, different methodologies will develop, and the value of works produced by this method will be evaluated.
| Published in | Innovation (Volume 5, Issue 3) |
| DOI | 10.11648/j.innov.20240503.11 |
| Page(s) | 83-89 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2024. Published by Science Publishing Group |
Music Composition, Data-Driven Method, Natural Science Data, Art
A | B | C | |
|---|---|---|---|
1 | 725089.562 | 4858.19877 | 31.9999306 |
2 | 725106.558 | 5834.75636 | 15.9999421 |
3 | 725129.562 | 4757.69794 | 47.9998495 |
4 | 725129.563 | 4815.48023 | 47.9998495 |
5 | 725138.558 | 4498.91418 | 47.9998843 |
6 | 725161.563 | 5008.25345 | 15.9999884 |
7 | 725166.06 | 5442.73808 | 24.9956829 |
8 | 725166.06 | 6416.53886 | 7.00428241 |
9 | 725170.558 | 6201.2257 | 15.9999769 |
10 | 725174.06 | 6442.4183 | 8.99569444 |
11 | 725176.567 | 4984.5126 | 31.999919 |
12 | 725177.562 | 5139.39887 | 47.9998727 |
13 | 725177.563 | 5166.94794 | 47.9998727 |
14 | 725178.558 | 5068.98451 | 31.9999074 |
15 | 725182.06 | 4676.20272 | 24.995625 |
16 | 725184.567 | 5317.83911 | 47.9998495 |
17 | 725186.558 | 4077.92379 | 15.9999306 |
18 | 725190.06 | 4477.67241 | 23.0041898 |
19 | 725197.064 | 5297.60197 | 8.9956713 |
20 | 725200.566 | 5588.51861 | 15.9999306 |
A | B | C | |
|---|---|---|---|
1 | 725090 | 4858 | 32 |
2 | 725107 | 5835 | 16 |
3 | 725130 | 4758 | 48 |
4 | 725130 | 4815 | 48 |
5 | 725139 | 4499 | 48 |
6 | 725162 | 5008 | 16 |
7 | 725166 | 5443 | 25 |
8 | 725166 | 6417 | 7 |
9 | 725171 | 6201 | 16 |
10 | 725174 | 6442 | 9 |
11 | 725177 | 4985 | 32 |
12 | 725178 | 5139 | 48 |
13 | 725178 | 5167 | 48 |
14 | 725179 | 5069 | 32 |
15 | 725182 | 4676 | 25 |
16 | 725185 | 5318 | 48 |
17 | 725187 | 4078 | 16 |
18 | 725190 | 4478 | 23 |
19 | 725197 | 5298 | 9 |
20 | 725201 | 5589 | 16 |
Column B | Frequency | Note | Offset cents | |
|---|---|---|---|---|
1 | 4858 | 4978.032 | D#8 | -42.25 |
2 | 5835 | 5919.911 | F#8 | -25 |
3 | 4758 | 4698.636 | D 8 | 21.73 |
4 | 4815 | 4698.636 | D 8 | 42.35 |
5 | 4499 | 4434.922 | C#8 | 24.83 |
6 | 5008 | 4978.032 | D#8 | 10.39 |
7 | 5443 | 5587.652 | F 8 | -45.40 |
8 | 6417 | 6271.927 | G 8 | 39.59 |
9 | 6201 | 6271.927 | G 8 | -19.68 |
10 | 6442 | 6271.927 | G 8 | 46.32 |
11 | 4985 | 4978.032 | D#8 | 2.42 |
12 | 5139 | 5274.041 | E 8 | -44.90 |
13 | 5167 | 5274.041 | E 8 | -35.49 |
14 | 5069 | 4978.032 | D#8 | 31.35 |
15 | 4676 | 4698.636 | D 8 | -8.35 |
16 | 5318 | 5274.041 | E 8 | 14.37 |
17 | 4078 | 4186.009 | C 8 | -45.25 |
18 | 4478 | 4434.922 | C#8 | 16.73 |
19 | 5298 | 5274.041 | E 8 | 7.84 |
20 | 5589 | 5587.652 | F 8 | 0.41 |
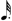 or
or 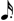 .
. 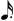 ). Since none can assign to 1, the composer arbitrarily assigns a note to it. Therefore, 1 is assigned to a 32nd note and a half. And hence: 1= a 64th note (
). Since none can assign to 1, the composer arbitrarily assigns a note to it. Therefore, 1 is assigned to a 32nd note and a half. And hence: 1= a 64th note ( 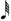 ). To recap, 25=
). To recap, 25= 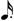 +
+ 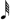 or
or 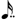 .
. 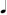 ) plus 3. The 3 can be three-fourths or
) plus 3. The 3 can be three-fourths or 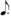 . Accordingly, the number 7 can be expressed in
. Accordingly, the number 7 can be expressed in 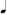 +
+ 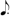 . However, it should be written as
. However, it should be written as 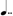 .
. 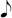 + 1. The number 1 can be converted into 1/8 (0.125). The value of 0.125 is too short to convert into a musical note. For extending the length, 9 can be converted into
+ 1. The number 1 can be converted into 1/8 (0.125). The value of 0.125 is too short to convert into a musical note. For extending the length, 9 can be converted into 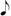 +
+ 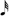 . The 18th row shows 23, or 16 (
. The 18th row shows 23, or 16 ( 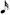 ) + 7. The 16 can halve as two 8s. The remainder, 7 can approximately turn into a 16th note (
) + 7. The 16 can halve as two 8s. The remainder, 7 can approximately turn into a 16th note ( 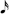 ) and 23 (
) and 23 ( 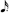 ).
). Data ‘C’ | 7 | 9 | 16 | 23 | 25 | 32 | 48 |
|---|---|---|---|---|---|---|---|
Notes |
|
B | C | Note | Lengths | |
|---|---|---|---|---|
1 | 4858 | 32 | D#8 | |
2 | 5835 | 16 | F#8 | |
3 | 4758 | 48 | D 8 | |
4 | 4815 | 48 | D 8 | |
5 | 4499 | 48 | C#8 | |
6 | 5008 | 16 | D#8 | |
7 | 5443 | 25 | F 8 | |
8 | 6417 | 7 | G 8 | |
9 | 6201 | 16 | G 8 | |
10 | 6442 | 9 | G 8 |
|
11 | 4985 | 32 | D#8 | |
12 | 5139 | 48 | E 8 | |
13 | 5167 | 48 | E 8 | |
14 | 5069 | 32 | D#8 | |
15 | 4676 | 25 | D 8 | |
16 | 5318 | 48 | E 8 | |
17 | 4078 | 16 | C 8 | |
18 | 4478 | 23 | C#8 | |
19 | 5298 | 9 | E 8 |
|
20 | 5589 | 16 | F 8 |
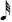 +
+ 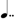 or
or 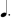 +
+ 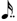 ), not out of proportion of the analysis of data.
), not out of proportion of the analysis of data. 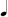 ) + 3 (
) + 3 ( 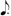 ) =
) = 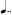 and 8 =
and 8 = 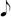 , threefold of 7. Basically, 7 should be at least less than
, threefold of 7. Basically, 7 should be at least less than 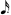 which is less than
which is less than 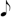 . To express 7 in lower notes than ones in which 8 is expressed, it would take more complex calculations—the process that will likely yield hundreds of notes. It will be excessively time-consuming. All these calls for the need for data liquidity. To inject personal philosophy and view into the composition, the composer needs to have consistency in data analysis
. To express 7 in lower notes than ones in which 8 is expressed, it would take more complex calculations—the process that will likely yield hundreds of notes. It will be excessively time-consuming. All these calls for the need for data liquidity. To inject personal philosophy and view into the composition, the composer needs to have consistency in data analysis | [1] | Stephen R Hoon (Manchester Metropolitan University) & B. K. Tanner (Durham University), The physics of music, Article in Physics Education, Phys. Educ., Vol 16. 1981 Printed In Great Britain, 1981. |
| [2] | Stephen Malloch and Colwyn Trevarthen, The Human Nature of Music, US National Library of Medicine National Institutes of Health Search database Search term, 2018. |
| [3] | Stanford Encyclopedia of Philosophy, Scientific Method, First published Fri Nov 13, 2015, |
| [4] | Stanford Encyclopedia of Philosophy, Enlightenment, First published Fri Aug 20, 2010; substantive revision Tue Aug 29, 2017. |
| [5] | Reginald Bain, The Harmonic Series - A path to understanding musical intervals, scales, tuning and timbre, University of South Carolina, 2003. |
| [6] | Philipp Brüllmann, Music Builds Character Aristotle, Politics VIII 5, 1340a14–b5, De Gruyter, 2013. |
| [7] | NASA Distributed Active Archive Center (DAAC) at NSIDC, GIMP Data (Greenland Ice Mapping Project), |
| [8] | MIT OpenCourseWare, 2.161 Signal Processing: Continuous and Discrete - For information about citing these materials or our Terms of Use, 2008. |
| [9] | Matthew Rankin, A Computer Model for the Schillinger System of Musical Composition, A thesis submitted in partial fulfillment of the degree of Bachelor of Science (Honours) at The Department of Computer Science Australian National University, 2012. |
| [10] | Leibniz, Mathematics illuminated Unit 10, Harmonious Math Textbook, 2017. |
| [11] | Joseph Schillinger, The Schillinger System of Musical Composition, The Musical Quarterly, Vol. 32, No 3, 1946. |
| [12] | John Haines and Patricia DeWitt, Johannes De Grocheio and Aristotellan Natural Philosophy, Cambridge University Press, 2008. |
| [13] | Janelle Anderson, Xenakis' Combination of Music and Mathematics, The Journal of Undergraduate Research - South Dakota State University, 2011. |
| [14] | James Q. Feng, Ph.D., Music in Terms of Science, 2012. |
| [15] | James Harley, The Creative Compositional Legacy of Iannis Xenakis, School of Fine art and Music, University of Guelph, 2006. |
| [16] | Iannis Xenakis & Additional Material compiled and edited by Sharon Kanach, Formalized Music – Thought and Mathematics in Composition, Harmonologia Series No. 6 – Pendragon Press Stuyvsant NY, 1992. |
| [17] | Ian Cross, Music and science: three views, University of Cambridge, 1998. |
| [18] | Frans Absil, A Guide to Schillinger’s Theory of Rhythm Second Edition, F. G. J. Absil, the Netherlands, 2015. |
| [19] | David R. Lapp, The Physics of Music and Musical Instruments, Wright Center for Innovative Science Education, Tufts University, 2003. |
| [20] | David J Hargreaves, Dorothy Miell, and RAYMOND A. R. MACDONALD, What are musical identities, and why are they important, Article, January 2002. |
| [21] | Christopher Dobrian, Realtime Stochastic Decision Making for Music Composition and Improvisation, 1966. |
| [22] |
Catherine Schmidt-Jones, Sound, Physics and Music, Online:
http://cnx.org/content/col10261/1.1/ Rice University, Houston, Texas, 2005. |
| [23] | A. Koblyakova, S. Petoukhov, I. Stepanian, The Genetic Code, the Golden Section and Genetic Music, The Moscow PI. Tchaikovsky Conservatory, 2015. |
APA Style
Lee, J. (2024). A New Music Composition Technique Using Natural Science Data. Innovation, 5(3), 83-89. https://doi.org/10.11648/j.innov.20240503.11
ACS Style
Lee, J. A New Music Composition Technique Using Natural Science Data. Innovation. 2024, 5(3), 83-89. doi: 10.11648/j.innov.20240503.11
AMA Style
Lee J. A New Music Composition Technique Using Natural Science Data. Innovation. 2024;5(3):83-89. doi: 10.11648/j.innov.20240503.11
@article{10.11648/j.innov.20240503.11,
author = {Joungmin Lee},
title = {A New Music Composition Technique Using Natural Science Data
},
journal = {Innovation},
volume = {5},
number = {3},
pages = {83-89},
doi = {10.11648/j.innov.20240503.11},
url = {https://doi.org/10.11648/j.innov.20240503.11},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.innov.20240503.11},
abstract = {The relationship of music and mathematics are well documented since the time of ancient Greece, and this relationship is evidenced in the mathematical or quasi-mathematical nature of compositional approaches by composers such as Xenakis, Schoenberg, Charles Dodge, and composers who employ computer-assisted-composition techniques in their work. This study is an attempt to create a composition with data collected over the course 32 years from melting glaciers in seven areas in Greenland, and at the same time produce a work that is expressive and expands my compositional palette. To begin with, numeric values from data were rounded to four-digits and converted into frequencies in Hz. Moreover, the other data are rounded to two-digit values that determine note durations. Using these transformations, a prototype composition was developed, with data from each of the seven Greenland-glacier areas used to compose individual instrument parts in a septet. The composition Contrast and Conflict is a pilot study based on 20 data sets. Serves as a practical example of the methods the author used to develop and transform data. One of the author’s significant findings is that data analysis, albeit sometimes painful and time-consuming, reduced his overall composing time. The variety and richness of data that exists from all academic areas and disciplines conceivably provide a rich reservoir of material from which to fashion compositions. As more composers explore this avenue of work, different methodologies will develop, and the value of works produced by this method will be evaluated.
},
year = {2024}
}
TY - JOUR T1 - A New Music Composition Technique Using Natural Science Data AU - Joungmin Lee Y1 - 2024/07/31 PY - 2024 N1 - https://doi.org/10.11648/j.innov.20240503.11 DO - 10.11648/j.innov.20240503.11 T2 - Innovation JF - Innovation JO - Innovation SP - 83 EP - 89 PB - Science Publishing Group SN - 2994-7138 UR - https://doi.org/10.11648/j.innov.20240503.11 AB - The relationship of music and mathematics are well documented since the time of ancient Greece, and this relationship is evidenced in the mathematical or quasi-mathematical nature of compositional approaches by composers such as Xenakis, Schoenberg, Charles Dodge, and composers who employ computer-assisted-composition techniques in their work. This study is an attempt to create a composition with data collected over the course 32 years from melting glaciers in seven areas in Greenland, and at the same time produce a work that is expressive and expands my compositional palette. To begin with, numeric values from data were rounded to four-digits and converted into frequencies in Hz. Moreover, the other data are rounded to two-digit values that determine note durations. Using these transformations, a prototype composition was developed, with data from each of the seven Greenland-glacier areas used to compose individual instrument parts in a septet. The composition Contrast and Conflict is a pilot study based on 20 data sets. Serves as a practical example of the methods the author used to develop and transform data. One of the author’s significant findings is that data analysis, albeit sometimes painful and time-consuming, reduced his overall composing time. The variety and richness of data that exists from all academic areas and disciplines conceivably provide a rich reservoir of material from which to fashion compositions. As more composers explore this avenue of work, different methodologies will develop, and the value of works produced by this method will be evaluated. VL - 5 IS - 3 ER -